Carlos M. Lorenzetti

Caracterización Formal y Análisis Empírico de Mecanismos Incrementales de Búsqueda basados en Contexto

Tesis Doctoral en Ciencias de la Computación - Universidad Nacional del Sur

por Carlos M. Lorenzetti

Similitud

La idea de definir un valor numérico para la similitud (o su inversa, la distancia) entre dos objetos, cada uno caracterizado por un conjunto común de atributos, es uno de los problemas fundamentales en IR y en otras áreas. Por ejemplo, en matemática se utilizan los métodos geométricos para medir la similitud en estudios de congruencia y homotecia, así como también en campos como la trigonometría [AMWW88]. Los métodos topológicos se aplican en campos como la semántica espacial [Kui00]. La teoría de grafos se usa ampliamente para evaluar las similitudes cladísticas en taxonomías [TWC98]. La teoría de grafos difusa también ha desarrollado sus propias métricas de similitud, que tienen aplicación en las más diversas áreas, como administración [DFF03], medicina [Adl86] y meteorología [MM85]. Medir la similitud de secuencias de pares de proteínas es un problema muy importante en la biología molecular [LP85].

La similitud también ha jugado un papel fundamental en experimentos psicológicos, por ejemplo, en experimentos con personas a las cuales se les pregunta acerca de la similitud de pares de objetos. En estos estudios se utilizan una gran variedad de técnicas, pero la más común es preguntar si los objetos son similares o no, o indicar en una escala el nivel de similitud que la persona piensa que tienen los objetos. El concepto de similitud también juega un rol fundamental en el modelado de tareas psicológicas, especialmente en teorías de reconocimiento, identificación y clasificación de objetos, como ser los gustos por ciertas marcas comerciales. Una suposición común es que cuando se está evaluando un producto, las personas se imaginan un producto ideal y luego juzgan la similitud de un producto nuevo con respecto a éste [Coo64].

Debido a la gran diversidad de áreas de aplicación que se mencionó más arriba, y a una falta de comunicación entre ellas, hubo mucho esfuerzo duplicado y, en general, los coeficientes más utilizados se reinventaron varias veces, existiendo diversos nombres para las mismas métricas. Algunos coeficientes son métricas de la distancia, o de la disimilitud entre los objetos, por lo que tienen un valor nulo para los objetos idénticos, mientras que otros miden directamente la similitud, y tienen un valor máximo para los objetos idénticos. Si la métrica tiene un rango $[0, 1]$ puede transformarse un coeficiente de similitud en un coeficiente de distancia complementario simplemente restándose el valor de similitud con la unidad, o calculando una inversa [BCK08]. En algunos casos una similitud y su complemento se desarrollaron de manera independiente y tienen nombres distintos.

Con una métrica de similitud pueden compararse dos documentos, dos consultas o un documento con una consulta. Entonces, esta medida puede ser una función que calcule el grado de similitud entre cualquier par de textos. También es posible crear un orden de los documentos recuperados por un sistema de IR a partir de esta medida. Esto es algo fundamental en la evaluación de muchos sistemas de IR. Dado que aún no existe la mejor métrica, existe un gran número de métricas de similitud propuestas en la literatura. Recopilar una lista completa es una tarea imposible, por lo que aquí nos concentraremos en las métricas más utilizadas o las más comunes en IR, y en particular en las utilizadas en esta tesis. Una recopilación de coeficientes de similitud puede encontrarse en [EFHW93].

Algunos métodos para resolver el problema del cálculo de la similitud incluyen: varios tipos de distancias de edición, o de Levenshtein [Lev65], entre dos términos. Esta distancia se define como la cantidad mínima de cambios necesarios en un término para transformarlo en el otro, en donde las operaciones permitidas se eligen de un conjunto fijo, como ser inserción o sustitución de una letra. También puede mencionarse la distancia de Hamming, entre dos cadenas de caracteres de la misma longitud. Se basa en [Ham50] y es igual a la cantidad de posiciones en las que difieren ambas cadenas. Asimismo existen distancias universales, o independientes de un modelo hipotético, como la distancia de información [BGL⁺98]; y métodos basados en algoritmos de compresión universales, para la estimación de la entropía relativa de pares de secuencias de símbolos [ZM93], o divergencia de Kullback-Leibler [KL51]. En un espacio multidimensional pueden definirse distancias entre pares de vectores en ese espacio, tales como la distancia Euclídea y la distancia de Manhattan. La primera se calcula como la norma Euclídea del vector diferencia de ambos vectores, y la última como la suma de las distancias en cada dimensión. La distancia de Hamming puede verse como la distancia de Manhattan entre vectores de bits [EMTB02]. En el Modelo Vectorial propuesto por Salton y visto en la Subsección 2.1.2, la medida de similitud más común es la similitud por coseno (Ecuación 2.1). A continuación se mencionarán algunas métricas muy utilizadas en el área y más adelante se detallará el concepto de similitud semántica.

Coeficiente de Jaccard

El coeficiente de similitud de Jaccard o índice de Jaccard mide la similitud entre dos conjuntos de muestras y fue concebido con la intención de comparar los tipos de flores presentes en un ecosistema de la cuenca de un río, con los tipos presentes en las regiones aledañas [Jac01]. Se define como la relación entre el tamaño de la intersección de ambos conjuntos y el tamaño de la unión:

La distancia de Jaccard mide la disimilitud entre dos conjuntos de muestras y se define como el complemento del coeficiente de Jaccard: $$J_{\delta}(A,B) = 1 - \mathit{sim}_J(A,B) = \frac{ |{A \cup B}| - |{A \cap B}| }{|{A \cup B}|}.$$ Muchos años después, Lee R. Dice, también en el campo de la Biología, propone una métrica relacionada con el coeficiente de Jaccard, conocida como coeficiente de Dice, para medir el nivel de relación que tienen dos especies animales comparada con una relación fortuita esperada [Dic45]:

Puede encontrarse la relación antes mencionada de la siguiente manera:

Para aplicar la Ecuación 2.9 para medir el grado de similitud entre un documento y una consulta debemos llevar o extender esta ecuación, que está expresada en función de conjuntos de términos, a una expresión en función de vectores de términos. Esta forma extendida del coeficiente de Jaccard también se conoce con el nombre de coeficiente de Tanimoto [Tan58]:

Expresada de esta forma es trivial ver que:

Similitud Okapi

La medida de similitud Okapi [SSMB95] es una de las métricas más populares en el campo de la IR tradicional y en varias conferencias de área [HBC99,RW99]. A diferencia de la Similitud por coseno del Modelo Vectorial, el método Okapi además de considerar la frecuencia de los términos de la consulta, también tiene en cuenta la longitud promedio de los documentos en la colección completa y la longitud del documento evaluado. En este método, la similitud entre una consulta $q$ y un documento $d_j$, puede describirse como el producto escalar del vector de la consulta $\overrightarrow{q}$ y el vector que describe el documento $\overrightarrow{d_j}$:
$$\begin{align*} sim_{o}(d_j, q) = \overrightarrow{q} . \overrightarrow{d_j} = \sum_{i = 1}^{m}{w(k_i,q) . w_{o}(k_i,d_j)}\text{,} \end{align*}$$
en donde $w(k_i,q)$ es la frecuencia de $i$-ésimo término de la consulta $q$ y $w_{o}(k_i,d_j)$ es el peso del documento de acuerdo a la siguiente expresión:
$$\begin{align}w_{o}(k_i,d_j) = \frac{\mathit{frec}(k_i,d_j) .\log ((N - n_i + 0.5)/(n_i + 0.5))}{2.(0.25 + 0.75.l(d_j)/\mathit{proml}) + \mathit{frec}(k_i,d_j) }\text{,} \end{align}$$ en donde $\mathit{frec}(k_i,d_j)$ es la frecuencia del $i$-ésimo término en el documento $d_j$, $N$ es el número de documentos en la colección, $n_i$ es el número de documento en la colección que contienen el término $k_i$ de la consulta, $l(d_j)$ es la longitud del documento (en bytes) y $\mathit{proml}$ es la longitud promedio de los documentos en la colección (en bytes).

La principal razón para tener en cuenta la longitud de los documentos en el cálculo del peso de los términos es que los documentos largos tienen más términos que los documentos cortos, por lo que los primeros tienen más probabilidades de ser recuperados que los segundos. La normalización que se incluye en la Ecuación 2.10 es una forma de reducir esta ventaja. Para aplicar esta métrica a la Web es necesario estimar el parámetro $\mathit{proml}$ [LSZ01].

Rango de Densidad de Cobertura

Existen otros métodos, como el Rango de Densidad de Cobertura (CDR), que en lugar de calcular la relevancia basándose en la aparición de los términos, se basan en la ocurrencia de frases [CCT00]. En CDR, los resultados de las consultas se ordenan en dos pasos:

1. Los documentos que poseen uno o más términos de la consulta $q$ se ordenan por su nivel de coordinación, o sea que aquellos que tengan más términos coincidentes estarán mejor posicionados. De esta manera los documentos quedarán agrupados y su ranking queda establecido por el grupo al que pertenecen. Los documentos con un nivel cero son descartados. Esto produce $n$ conjuntos, en donde $n$ es igual a la cantidad de términos de la consulta $q$.
2. Los documentos dentro de cada grupo se ordenan para producir un orden general. Este se basa en la proximidad y en la densidad de los términos de la consulta dentro de cada documento. Cada documento $d_h$ se convierte en una lista ordenada de términos $k_1, k_2, \dots, k_m$ con sus posiciones $1, \dots, m$, en donde $m$ es la cantidad de términos del documento. Luego se calculan las coberturas, que consisten de pares ordenados de la forma $(i, j)$ tales que $i < j$ y $k_i, k_j \in q$ que sean lo más cortos posibles, es decir, que no existe otra cobertura $({i'}, {j'})$ tal que $i < i' < j' < j$. Finalmente se define el conjunto cobertura $\omega(d_h) = {({i_1}, {j_1}), ({i_2}, {j_2}), \dots,({i_c}, {j_c})}$, en donde $c$ representa la cantidad de coberturas encontradas, y se calcula un puntaje para cada documento, $S(\omega)$, de la siguiente manera:
   $$ \begin{align} S(\omega ) &= \sum\limits_{z = 1}^{c}{I(\omega_z)} = \sum\limits_{z = 1}^{c}{I({i_z}, {j_z})}\text{,}\end{align}$$

   en donde $I(i,j)$ está definido de la siguiente manera:

   $$\begin{align} I(i, j) &= \begin{cases} \frac{\lambda}{{j - i + 1}}\text{,} & \text{si }(j - i + 1) > \lambda \text{,} \\ 1\text{,} & \text{en otro caso.} \end{cases} \end{align}$$
   En la fórmula de arriba $\lambda$ es una constante, en particular en [CCB95] se utilizó $\lambda = 16$, obteniendo buenos resultados para consultas booleanas. La Ecuación 2.12 le asigna un peso de 1 a las coberturas cuya longitudes sean iguales o menores a $\lambda$ y, a las mayores, les asigna un peso menor a 1 que es proporcional a la inversa del intervalo entre los términos.

La Ecuación 2.11 puede interpretarse como una función de similitud, aunque su rango va a depender de $\omega$ y del $\lambda$ elegido. Un ejemplo puede encontrarse en [CCT00]. El beneficio de este método es que no sólo tiene en cuenta el número de términos distintos dentro de un documento, sino qué tan cerca están unos de otros. Esto puede resultar acorde a las expectativas de un usuario que, en general, busca que las palabras ingresadas estén cercanas en los documentos recuperados.

Método de Puntaje de Tres niveles

El Método de Puntaje de Tres niveles (TLS) está diseñado para tener en cuenta las expectativas del usuario acerca de los resultados de la búsqueda y su modelo se basa en algunos métodos manuales existentes. Muchos métodos manuales usan el siguiente criterio para asignar puntajes de relevancia [CR96,LS99]:

1. Los enlaces relevantes, aquellos que están relacionados con las necesidades de información de una consulta, o los que tienen enlaces a otras páginas que pueden ser útiles para la consulta, obtienen 2 puntos.
2. Los enlaces que son ligeramente relevantes, aquellos que sólo están un poco relacionados con una consulta, aquellos con una definición muy corta que es útil, o que contienen soluciones técnicas a un problema que es relevante para la consulta, o contienen alguna descripción de un trabajo relacionado, obtienen 1 punto.
3. Los siguientes enlaces obtienen 0 puntos:
   • Enlaces duplicados. Este tipo no tiene en cuenta a los sitios espejo.
   • Los enlaces inactivos, que son aquellos que producen algún tipo de mensaje de error. Por ejemplo, error de ``archivo no encontrado'', ``prohibido'' o ``el servidor no responde''.
   • Enlaces irrelevantes, o sea aquellos que contienen información irrelevante para la consulta.

Este método calcula la relevancia de una página Web con una consulta de la siguiente manera:

• Dada una frase de consulta $q$ con $n$ términos y una página Web $d_j$, se calcula un primer puntaje para esa página como:
  $$\begin{align*} A(d_j, q) = \frac{f_n . k^{n-1} + f_{n-1} . k^{n-2} + \dots + f_1}{k^{n-1}}\text{,} \end{align*}$$
  en donde $k$ es una constante y $f_i$, $1 \leq i \leq n$ es el número de subfrases de longitud $i$, o sea, que contienen $i$ términos de $q$ en $d_j$. El orden de los términos en cada subfrase tiene que ser el mismo que en la consulta.
• Se convierte $A(d_j, q)$ en un puntaje de similitud de tres niveles por medio de un umbral, de forma de asignar 2 puntos a los documentos relevantes, 1 punto a los parcialmente relevantes y 0 puntos a los irrelevantes:
  $$\begin{align*} \mathit{sim}_{TLS}(d_j, q) = % \begin{cases} 2\text{,} & \text{si }A(d_j, q) \geq \Theta\text{,}\\ 1\text{,} & \text{si }\Theta > A(d_j, q) \geq \alpha\Theta\text{,}\\ 0\text{,} & \text{si }A(d_j, q) < \alpha\Theta\text{.}\\ \end{cases} \end{align*}$$
  en donde $\Theta$ es una constante de umbral para considerar a un documento relevante, y $\alpha$ es un valor entre $0$ y $1$ que representa el porcentaje de $\Theta$ que se pide para que un documento sea parcialmente relevante.

Entre las ventajas de este método se pueden mencionar que califica mejor a los documentos que tengan más términos coincidentes, y que también considera el orden de aparición de esos términos en el documento, ya que el orden puede cambiar el significado de una frase [LSZ02].

A continuación se muestra un ejemplo ilustrativo simple. En la consulta ``procesamiento paralelo distribuido'', hay 1 frase con 3 términos (procesamiento paralelo distribuido), 3 subfrases con 2 términos (procesamiento paralelo, paralelo distribuido, procesamiento distribuido) y 3 subfrases con 1 término (procesamiento, paralelo, distribuido). Supongamos que existe una página Web tal que, el número de apariciones de la frase exacta de la consulta es $f_3=2$, el número total de apariciones de subfrases con dos términos es $f_2=7$, y que número total de apariciones de subfrases con un término es $f_1=18$. Si ajustamos los tres parámetros del algoritmo a $\Theta=1$, $\alpha=0.1$, y $k=10$, obtenemos $ A=(2{.}10^2+7{.}10+18)/10^2=2.88$, y $sim_{TLS}=2$.

Similitud semántica

El desarrollo de mecanismos de búsqueda web está fuertemente condicionado a resolver los siguientes interrogantes: (1) ¿cómo encontrar páginas relevantes? y, (2) dado un conjunto de páginas web potencialmente relacionadas, ¿cómo ordenarlas de acuerdo a su relevancia? Para evaluar la efectividad de un mecanismo de búsqueda web en estos aspectos se necesitan medidas de similitud semántica. La similitud semántica, al igual que en caso de la similitud, puede utilizarse para comparar objetos en las áreas más diversas. En esta tesis en particular está relacionada con el cálculo de la similitud entre documentos, que a pesar de estar descriptos con vocabularios diferentes y por lo tanto ser léxicamente diferentes, son similares conceptualmente [HVV⁺06].

En los mecanismos tradicionales las similitudes, o juicios de relevancia, son proporcionadas por los usuarios de forma manual, lo cual como se mencionó anteriormente, es muy difícil de obtener. Más importante aún es el problema de la escalabilidad, ya que en grandes colecciones de datos como la Web es imposible cubrir exhaustivamente todos los tópicos existentes. El Open Directory Project (ODP) es un gran directorio de la Web editado por personas, y utilizado por cientos de portales y sitios de búsqueda. El ODP clasifica millones de URLs en una ontología temática. Las ontologías ayudan a darle sentido a un conjunto de objetos y, con esta información, pueden derivarse relaciones semánticas entre esos objetos. Por lo tanto, el ODP es una fuente muy útil de donde se pueden obtener medidas de similitud semántica entre páginas web.

Una ontología es un tipo especial de red. El problema de evaluar la similitud semántica en una red tiene una larga historia en la teoría psicológica [Tve77]. Más recientemente, la similitud semántica se ha vuelto algo fundamental en la representación de conocimiento, en donde este tipo especial de redes se utilizan para describir objetos y sus relaciones [Gru93].

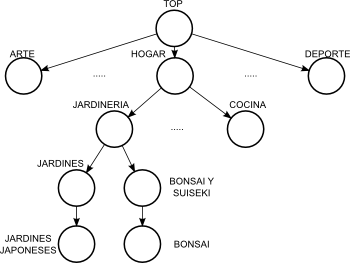
Existen muchas propuestas para medir la similitud semántica por medio del cálculo de distancia entre nodos en una red. La mayoría se basan en la premisa de que mientras más relacionados semánticamente estén dos objetos, más cerca deberán estar en la red. Sin embargo, tal como ha sido discutido por varios autores, surgen problemas al utilizar medidas basadas en distancia en redes en las cuales los enlaces no representan distancias uniformes [Res95]. Un ejemplo de esto puede verse en la porción del ODP que se muestra en la Figura 2.9, en donde el tópico Jardines Japoneses se encuentra a la misma distancia del tópico Cocina que del tópico Bonsai, pero es claro que la relación semántica con el último es más fuerte que con el primero. La diferencia radica en el ancestro común más próximo a ambos pares, que en el caso de ``Jardines Japoneses'' y ``Bonsai'' es Jardinería que es más específico que Hogar, el ancestro común con el otro tópico.

Figura 2.9: Porción de una taxonomía de tópicos.

En las ontologías algunos enlaces conectan categorías muy densas y generales, mientras que otros a categorías muy específicas. Para resolver este problema algunas propuestas estiman la similitud semántica basándose en la noción de contenido de información [Res95,Lin98]. La similitud entre dos objetos se asocia con sus similitudes y con sus diferencias. Dado un conjunto de objetos en una taxonomía ``es-un'', la similitud entre dos objetos puede estimarse encontrando el ancestro común más cercano.

Las ontologías a veces son consideradas como taxonomías ``es-un'', pero no están limitadas a esta forma. Por ejemplo, la ontología ODP es más compleja que un árbol simple. Algunas categorías tienen múltiples criterios para clasificar sus subcategorías. La categoría ``Negocios'', por ejemplo, está subdividida en tipos de organizaciones (cooperativas, negocios pequeños, grandes compañías), así como también en áreas (automotores, cuidado de la salud, telecomunicaciones). Además, el ODP tiene varios tipos de enlaces de referencias cruzadas entre categorías, por lo cual cada nodo puede tener varios nodos padre e incluso pueden existir ciclos.

Las medidas de similitud semántica que se basan en árboles son muy estudiadas [GGMW03], sin embargo el diseño de medidas bien fundamentadas para objetos almacenados en nodos de grafos arbitrarios es un problema abierto.

Similitud basada en Árboles

Lin [Lin98] ha investigado una definición de similitud basada en la teoría de la información que es aplicable en tanto el dominio tenga un modelo probabilístico. Esta propuesta puede utilizarse para derivar una medida de similitud semántica entre tópicos en una taxonomía ``es-un''.

De acuerdo a esta propuesta, la similitud semántica se define como una función del significado que comparten los tópicos y el significado de cada tópico de forma individual. En una taxonomía, el significado que se comparte puede hallarse buscando el ancestro común más cercano a los dos tópicos. Una vez que se tiene identificada esta clasificación común se puede medir el significado como la cantidad de información que se necesita para alcanzar ese estado. Asimismo, el significado de cada tópico se mide como la cantidad de información que se necesita para describirlo en forma completa.

En el campo de la teoría de la información [CT91], el contenido de información de una clase o tópico $\tau$ se mide como el negativo del logaritmo de una probabilidad $- log Pr[\tau]$.

en donde $\tau_0 (\tau_{1}, \tau_2 )$ es el tópico ancestro común más cercano en el árbol para los tópicos $\tau_1$ y $\tau_2$, y $\Pr [\tau]$ representa la probabilidad a priori de que cualquier página sea clasificada bajo el tópico $\tau$.

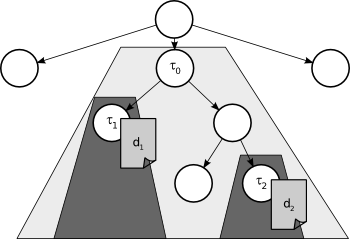
Dado un documento $d_j$ que está clasificado en un tópico de la taxonomía, utilizamos $mathfrak{T}(d_j)$ para referirnos al nodo del tópico que contiene a $d_j$. Dados dos documentos $d_1$ y $d_2$ en una taxonomía de tópicos, la similitud semántica entre ellos se estima como $\mathit{sim}_s^T (\mathfrak{T}(d_1) ,\mathfrak{T}(d_2) )$. Para simplificar la notación usaremos $\mathit{sim}_s^T (d_1 ,d_2 )$ en lugar de la expresión anterior. De aquí en adelante nos referiremos a $\mathit{sim}_s^T$ como la medida de similitud semántica basada en árboles. Un ejemplo de esta medida se muestra en la Figura 2.10. Allí los documentos $d_1$ y $d_2$ están contenidos en los tópicos $\tau_1$ y $\tau_2$ respectivamente, mientras que el tópico $\tau_0$ es su ancestro común más cercano. En la práctica $Pr [\tau]$ puede calcularse, para cada tópico $\tau$ en la ontología ODP, contando la \fracción de páginas que están almacenadas en el subárbol cuya raíz es el nodo $\tau$ (que llamaremos $subtree(\tau)$) respecto de todas las páginas del árbol.

Figura 2.10: Ejemplo de similitud semántica basada en un árbol.

Esta medida tiene varias propiedades interesantes y una sólida justificación teórica. Es la extensión directa de la medida de similitud de teoría de información [Lin98], diseñada para compensar el desbalanceo del árbol en cuanto a los términos de su topología y en cuanto al tamaño relativo de sus nodos. En un árbol balanceado perfectamente $\mathit{sim}_s^T$ se corresponde con la medida clásica de distancia en árboles [KT99].

En [Men04a,Men04b,Men05] se calculó la medida $\mathit{sim}_s^T$ para todos los pares de páginas de una muestra por capas de alrededor de 150.000 páginas del ODP. Para cada uno de los $3.8 \times 10^9$ pares resultantes también se calcularon las medidas de similitud del texto y de los enlaces, y se hizo una correlación entre éstas y la similitud semántica. Un resultado interesante es que estas correlaciones fueron un poco débiles sobre todos los pares, pero se fortalecieron en páginas dentro de algunas categorías de los niveles altos, como ``Noticias'' y ``Referencia''.

Dado que $\mathit{sim}_s^T$ sólo está definida en término de los componentes jerárquicos del ODP no es buena a la hora de capturar muchas de las relaciones semánticas inducidas por otros componentes (enlaces simbólicos y relacionados). Es por esto que la similitud semántica basada en árboles entre las páginas que pertenecen a los tópicos de los niveles superiores es cero, incluso si los tópicos están claramente relacionados. Esto muestra un escenario poco confiable al considerar todos los tópicos de la ontología, como sería por ejemplo, la Figura 2.11.

Figura 2.11: Porción de una ontología de tópicos.

En la figura puede verse que si sólo se consideran los enlaces de la taxonomía, la similitud semántica entre los tópicos Hogar/.../Bonsai y Compras/.../Bonsai sería cero, lo cual claramente no refleja la fuerte relación que existe entre ambos. Es por esto que es necesario definir una métrica que contemple todos los tipos de relaciones que encontramos en las ontologías.

Similitud basada en Grafos

Si generalizamos la medida de similitud semántica para que tenga en cuenta grafos arbitrarios, necesitamos definir una medida $\mathit{sim}_s^G$ que saque provecho de los componentes jerárquicos y no jerárquicos de una ontología.

Un grafo de una ontología temática es un grafo de nodos que representan tópicos. Cada nodo contiene objetos que representan documentos (páginas). Está constituido por un componente jerárquico (árbol) compuesto por enlaces ``es-un'' y un componente no jerárquico compuesto por enlaces cruzados de distintos tipos.

Por ejemplo, la ontología ODP es un grafo dirigido $G = (V,E)$ en donde:

• $V$ es un conjunto de nodos que representan los tópicos que contienen documentos;
• $E$ es un conjunto de aristas entre los nodos de $V$, divididos en tres subconjuntos $T$, $S$ y $R$ tales que:
  • $T$ es el componente jerárquico de la ontología,
  • $S$ es el componente no jerárquico compuesto de enlaces cruzados ``simbólicos'',
  • $R$ es el componente no jerárquico compuesto de enlaces cruzados ``relacionados''.

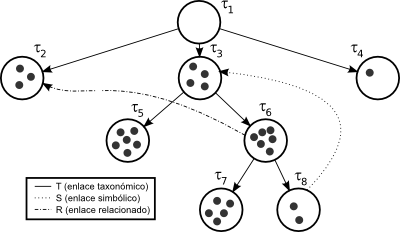
La Figura 2.12 muestra un ejemplo simple de un grafo G definido por los conjuntos $V = {\tau_1, \tau_2, \tau_3, \tau_4, \tau_5, \tau_6, \tau_7, \tau_8}$, $T = { (\tau_1, \tau_2 ), (\tau_1, \tau_3), (\tau_1, \tau_4), (\tau_3, \tau_5), (\tau_3, \tau_6), (\tau_6, \tau_7), (\tau_6, \tau_8) }$, $S = { (\tau_8, \tau_3) }$, y $R = { (\tau_6, \tau_2) }$. Además, cada nodo $\tau \in V$ contiene un conjunto de objetos. El número de objetos almacenados en un nodo $\tau$ se representa como $|{\tau}|$ (p. ej., $|{ \tau_3 }| = 4$).

Figura 2.12: Ejemplo de una ontología.

La extensión de la métrica $\mathit{sim}_s^T$ para considerar grafos genera dos interrogantes. La primera, ¿cómo buscar el ancestro común más específico de un par de tópicos en un grafo?; y la segunda, ¿cómo extender la definición de subárbol con raíz en un tópico dado?

Una diferencia importante entre las taxonomías y las ontologías, como el grafo ODP, es que en las primeras las aristas son todas del mismo tipo (enlaces ``es-un''), mientras que en las segundas pueden existir distintos tipos (p. ej., ``es-un'', ``simbólico'', ``relacionado''). Los distintos tipos de aristas tienen diferentes significados y deberían ser utilizados coherentemente. Una forma de distinguir el rol de las aristas es asignarles pesos y variarlos de acuerdo a su tipo. El peso de una arista $w_{ij} \in [0, 1]$ entre los tópicos $\tau_i$ y $\tau_j$ puede interpretarse como una medida explícita del grado de pertenencia de $\tau_j$ a la familia del tópico cuya raíz es $\tau_i$. Los enlaces ``es-un'' y los ``simbólicos'', en ODP, tienen el mismo peso ya que, como no se permiten los enlaces repetidos, estos últimos son la única manera de representar membresías múltiples. Por otro lado, los enlaces ``relacionados'' suponen una relación más débil.

Se asume que $w_{ij} > 0$ si y sólo si existe algún tipo de arista entre los tópicos $\tau_i$ y $\tau_j$. Sin embargo, para estimar la pertenencia a un tópico deben considerarse relaciones transitivas entre las aristas.

• $e_1 = (\tau_i, \tau_k)$ para algún $\tau_k \in V$;
• $e_n = (\tau_k, \tau_j)$ para algún $\tau_k \in V$;
• $e_k \in T\cup S\cup R$ para $k = 1\dots n$; y
• $e_k \in S\cup R$ a lo sumo para un $k$.

Las condiciones anteriores expresan que $\tau_j \in \tau_{i}\hspace{-1.2mm}\downarrow$ si hay un camino directo desde $\tau_i$ a $\tau_j$ en el grafo $G$, en donde a lo sumo una arista de $S$ o de $R$ está contenida en ese camino. Esta última condición es necesaria por tres motivos. Primero, si se permiten más aristas, el cómputo no podría llevarse a cabo, ya que en la práctica cualquier tópico podría pertenecer a cualquier otro. Segundo, se perdería robustez, porque algunos enlaces cruzados producirían grandes cambios en todas las membresías. Finalmente y más importante, haría que la clasificación de un tópico pierda sentido al mezclar todos los tópicos unos con otros. Los distintos tópicos $\tau_j$ ahora están asociados a lo que denominamos el cono $\tau_{i}\hspace{-1.2mm}\downarrow$ de un tópico $\tau_i$ con diferentes grados de pertenencia.

La estructura del grafo se puede representar como matrices de adyacencia. La matriz $\mathbf{T}$ representa la estructura jerárquica de la ontología y es equivalente a las aristas de $T$ a las que se le agregan 1s en la diagonal. Los componentes no jerárquicos de la ontología se representan con la matriz $\mathbf{S}$ y con la matriz $\mathbf{R}$, como se muestra a continuación.

Se calcula la matriz $\mathbf{G} = \mathbf{T}\vee \mathbf{S}\vee \mathbf{R}$, que es la matriz de adyacencia del grafo $G$ a la que se le agregaron 1s en la diagonal.

Entonces se define:

y la clausura de $\mathbf{T}$, $\mathbf{T}^{+}$, como:

En esta matriz, $\mathbf{T}^{+}_{ij} = 1$ si $\tau_{j}\in subtree(\tau_i)$ y si no es cero.

Finalmente se calcula la matriz $\mathbf{W}$ de la siguiente manera:

Cada elemento $\mathbf{W}_{ij}$ puede interpretarse como un valor de pertenencia difusa del tópico $\tau_{j}$ al cono $\tau_{i}\hspace{-1.2mm}\downarrow$ y luego se puede ver a $\mathbf{W}$ como la matriz de pertenencia difusa de $G$.

A modo de ejemplo consideremos a la ontología que se mostró en la Figura 2.12. En este caso las matrices $\mathbf{T}$, $\mathbf{G}$, $\mathbf{T}^{+}$ y $\mathbf{W}$ están definidas de la siguiente manera:

Entonces la similitud semántica entre dos tópicos $\tau_1$ y $\tau_2$ en un grafo de una ontología puede calcularse de la siguiente manera.

Definición 11 [MMRV05] Sean dos tópicos $\tau_1$ y $\tau_2$ en un grafo dirigido $G=(V,E)$, con $V$ el conjunto de nodos que representan a los tópicos que contienen documentos y $E$ el conjunto de aristas. ${|{ U }|}$ representa el número de documentos en el grafo. Sea $\Pr [\tau_k ]$ la probabilidad a priori de que un documento cualquiera sea clasificado en un tópico $\tau_k$ y se calcula como:

Sea $\Pr [\tau_i |\tau_k ]$ la probabilidad posterior de que cualquier documento será clasificado en un tópico $\tau_i$ luego de ser clasificado en $\tau_k$, y se calcula:

Quedando finalmente,

La definición $\mathit{sim}_S^G$ es una generalización de $\mathit{sim}_S^T$, ya que si se da el caso de que $G$ sea un árbol ( $S = R = \emptyset$), entonces $cone{i}$ es igual a $subtree(\tau_i)$, el subárbol del tópico cuya raíz es $\tau_i$, y todos los tópicos $\tau \in subtree(\tau_i)$ pertenecen a $cone{i}$ con un grado igual a 1. Si $\tau_k$ es un ancestro de $\tau_1$ y $\tau_2$ en una taxonomía, entonces $min (\mathbf{W}_{k1} ,\mathbf{W}_{k2} ) = 1$ y $Pr [\tau_i \vert\tau_k ] \cdot Pr [\tau_k ] = Pr [\tau_i ]$ para $i = 1, 2$.

Resumen

En este capítulo se definieron los fundamentos de los sistemas de IR que serán utilizados en los capítulos siguientes de esta tesis. Entre ellos, los modelos clásicos de representación en IR, como son el modelo Booleano, el Vectorial, el Probabilístico y el Indexado por Semántica Latente. Luego se explicó el proceso de generación de una consulta, los mecanismos más usados para reformulación de consultas y el concepto de realimentación de relevancia. Finalmente se mostraron dos conceptos fundamentales para el desarrollo de esta tesis, la similitud y la similitud semántica. Se analizaron las métricas más comunes en el área y se definió la noción de similitud semántica basada en árboles, mostrándose sus limitaciones. En vista de esto se definió la similitud semántica basada en grafos, una métrica que tiene en cuenta los distintos tipos de enlaces presentes en una ontología, y que es capaz de medir más fielmente las relaciones existentes entre tópicos relacionados conceptualmente.

Capítulo 3 ->