Carlos M. Lorenzetti

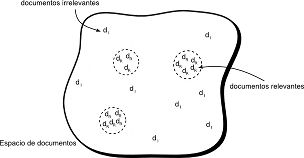
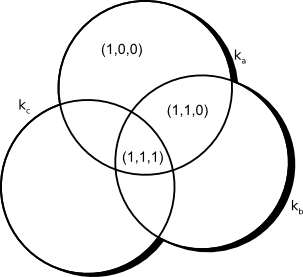
Caracterización Formal y Análisis Empírico de Mecanismos Incrementales de Búsqueda basados en Contexto

Tesis Doctoral en Ciencias de la Computación - Universidad Nacional del Sur

por Carlos M. Lorenzetti

Fundamentos

Modelos para Recuperación de Información

Los modelos de IR clásicos consideran que un documento está representado por un conjunto representativo de palabras claves, llamadas términos índice. Esta idea fue sugerida por Luhn en los '50s [Luh57]. Un término índice es una palabra simple dentro de un documento, cuya semántica nos ayuda a recordar los temas principales sobre los que trata el documento (de ahora en más nos referiremos a estas palabras simplemente como términos de un documento, excepto que se indique lo contrario). Por lo tanto, se los utiliza tanto para indexar como para resumir el contenido de un documento. Se trata generalmente de sustantivos, porque ellos tienen un significado y su semántica es fácil de identificar y comprender. Otros tipos de términos, como son los adjetivos, los adverbios y los conectores no son tan útiles para realizar índices porque se utilizan como complementos de los sustantivos. Sin embargo es interesante considerar todas las palabras en un documento a la hora de realizar un índice. Algunos motores de búsqueda utilizan esta idea de indexado de texto completo.

Dado un conjunto de términos de algún documento se puede notar que no todos son igualmente útiles a la hora de describir el documento. De hecho, hay algunos que son mucho más vagos que otros. No es un problema trivial decidir la importancia de un término como condensador del contenido de un documento. Más allá de esto, hay algunas propiedades de un término que son mensurables con facilidad y que son útiles para evaluar su potencialidad. Por ejemplo, consideremos una colección (o corpus) que contiene cien mil documentos. Una palabra que aparece en cada uno de los cien mil documentos es absolutamente inútil como término porque no nos dice nada acerca de cuáles documentos podrían interesarle a un usuario. Pero, otra palabra que aparezca en sólo cinco documentos sería más útil, porque reduce considerablemente el espacio de documentos que podría ser de interés para un usuario. Esto muestra que los distintos términos tienen una relevancia variable al usarlos para describir el contenido de los documentos.

Ahora vamos a definir la noción de peso de un término en un documento. Sea un término $k_i$, un documento $d_j$ y el peso asociado a $(k_i, d_j)$, $w(k_i,d_j)\geq 0$. Este peso es una estimación de la importancia del término como descriptor del contenido semántico de un documento.

Definición 1 [Sal71, BYRN99] Sea $t$ el número de términos en un corpus $C$ y $k_{i}$ un término cualquiera. Entonces $K=\{ k_{1}, \dots, k_{t}\}$ es el conjunto de términos. Se asocia un peso $w(k_i,d_j)>0$ a cada término $k_{i}\in d_{j}$ y $w(k_i,d_j)=0$ si $k_{i}\notin d_{j}$. Dado un documento $d_{j}$ se le asocia un vector de términos $\overrightarrow{d_j}$ que representa $\overrightarrow{d_j} = (w(k_1, d_j), w(k_2, d_j), \dots, w(k_t, d_j))$. Además, sea $g_i$ una función que devuelve el peso asociado con un término $k_i$ de cualquier vector de $t$ dimensiones, o sea, $g_i(\overrightarrow{d_j}) = w(k_i, d_j)$.

Como mencionaremos más adelante, se asume que los pesos de los términos son mutuamente independientes, lo que significa que el peso $w(k_i, d_j)$ asociado a $(k_{i}, d_{j})$ no está relacionado con el peso $w(k_{i+1}, d_j)$ asociado al término $i+1$ del mismo documento. Se asume, por lo tanto, que la aparición de un término no está correlacionada con la ocurrencia de otro, lo que es claramente una simplificación del modelo. Un ejemplo que contradice esta simplificación son, p. ej. los términos red y computadora, que podrían aparecer en un documento relacionado con las redes de computadoras. En este documento seguramente aparecerá uno de estos términos muy cerca del otro. Luego, puede verse que estas palabras están correlacionadas y esta relación podría reflejarse en sus pesos. La independencia mutua es una gran simplificación, pero reduce los cálculos de los pesos y agiliza el cálculo del ranking de los documentos.

En un entorno en el que se quieren recuperar documentos, o en cualquier otro relacionado con coincidencia de patrones, en donde las entidades almacenadas (documentos) se comparan unas con otras o con nuevos patrones (pedidos de búsqueda), el mejor espacio de indexación es uno en el cual cada entidad está tan alejada como sea posible una de otra; en estas circunstancias la calidad de un sistema de indexado se puede expresar como una función de la densidad del espacio de objetos; en particular, el rendimiento en la recuperación puede correlacionarse inversamente con la densidad espacial [SWY75].

La pregunta que surge es si existe un espacio de documentos óptimo, esto es, uno que produzca un rendimiento óptimo en la etapa de recuperación. La configuración del espacio de documentos es una función de la forma en la que se asignan los términos y sus pesos a los documentos de una colección. Si no se tiene ningún conocimiento especial sobre los documentos a indexar, se podría suponer que un espacio ideal de documentos es uno en donde los documentos más relevantes para ciertas consultas están agrupados, asegurando que se recuperen de forma conjunta al ingresar las mismas. De esta manera, aquellos documentos que no se quieren recuperar deberían estar muy separados en ese espacio. Esa situación se muestra en la Figura 2-1, en donde la distancia entre dos documentos (representados con “$d_{r}$” si son documentos relevantes y con “$d_{i}$” si son documentos irrelevantes) está inversamente relacionada con la similitud entre los vectores correspondientes.

Figura 2-1: Espacio de documentos ideal.

La configuración que muestra la Figura 2-1 representa la mejor situación posible, en la que los ítems que son relevantes e irrelevantes para varias consultas son separables, pero no existe una forma práctica de producir tal espacio, porque durante la etapa de indexado es muy difícil anticipar los juicios de relevancia de los usuarios a lo largo del tiempo. Esto quiere decir que la configuración óptima es muy difícil de generar si no se tiene un conocimiento a priori de una colección de documentos dada.

Las definiciones que acabamos de dar nos ayudarán a discutir cuatro modelos clásicos de IR, el modelo Booleano, el Vectorial, el Probabilístico y el Indexado de Semántica Latente.

Modelo Booleano

El modelo Booleano es el modelo de recuperación más simple y se basa en la teoría de conjuntos y en el álgebra de Boole. El modelo Booleano proporciona una arquitectura fácil de comprender para un usuario común de un sistema de IR, ya que los conceptos de conjuntos son bastante intuitivos. Las consultas expresadas como expresiones de Boole tienen una semántica precisa. El modelo Booleano recibió una gran atención y fue adoptado por muchos sistemas bibliográficos comerciales debido, principalmente, a su inherente simplicidad y a su formalismo puro.

A pesar de esto, el modelo sufre de grandes desventajas. La primera es que su estrategia de recuperación se basa en un criterio de decisión binario; un documento es relevante o no lo es (la noción de relevancia se analiza en la Sección 3.4.1). No existe la noción de grado de relevancia, lo que evita que el modelo tenga un buen rendimiento en la recuperación de grandes volúmenes de información. Tal es así que este modelo es más un modelo de recuperación de datos que uno de recuperación de información. La segunda desventaja reside en la representación de las consultas, que como se dijo, tienen una semántica precisa pero no es tan simple transformar una idea de un usuario en una expresión Booleana. De hecho, la mayoría de los usuarios encuentran a este proceso muy dificultoso e incómodo y las expresiones Booleanas que formulan tienden a ser bastante simples. A pesar de estos problemas, el modelo Booleano continúa siendo popular en bases de datos de documentos médicos [KZPS09] y legales [OHTB08] siendo un buen punto de partida para el estudio de los conceptos básicos de IR.

El modelo considera que los términos están presentes o están ausentes en un documento. Es por ello que los pesos de los términos son todos binarios, o sea, $w(k_i, d_j) \in {0,1}$. Una consulta $q$ puede estar compuesta de términos unidos entre sí por conectores lógicos: $not$, $and$ y $or$. Por lo tanto, una consulta es esencialmente una expresión Booleana convencional que puede ser representada como una disyunción de vectores conjuntivos, esto es, en la Forma Normal Disyuntiva o DNF. Por ejemplo, si consideramos la consulta $[q = k_a \wedge (k_b \vee \not k_c)]$, esta puede escribirse (analizando su tabla de verdad) en la forma normal disyuntiva como $\overrightarrow{q_{dnf}} = (1, 1, 1) \vee (1, 1, 0) \vee (1, 0, 0)$, en donde cada uno de los componentes es un vector binario de pesos asociado con la tupla $(k_a, k_b, k_c)$. Estos vectores binarios de pesos se llaman componentes conjuntivos de $q_{dnf}$. La Figura 2-2 muestra los tres componentes conjuntivos para el ejemplo.

Figura 2-2: Componentes de una consulta booleana.

Definición 2 [LF73, BYRN99] En el modelo Booleano, los pesos de los términos son todos valores binarios, esto es, $w(k_i, d_j) \in {0, 1}$. Una consulta $q$ es un expresión Booleana normal. Sea $\overrightarrow{q_{dnf}}$ la forma normal disyuntiva de la consulta $q$. Además, sea $\overrightarrow{q_{cc}}$ cualquiera de los componentes conjuntivos de $\overrightarrow{q_{dnf}}$. Luego, la similitud entre un documento $d_j$ y una consulta $q$ está definida como:
$$ \mathit{sim}_{bool}(d_{j}, q) = \begin{cases} 1\text{,} & \text{si }\exists\overrightarrow {q_{\mathit{cc}}} | (\overrightarrow {q_{\mathit{cc}}} \in \overrightarrow {q_{\mathit{dnf}}}) \wedge ({\forall _{{k_i}}},g_i(\overrightarrow{d_j}) = g_i(\overrightarrow{q_{cc}}))\text{,}\\ 0\text{,} & \text{si no.} \end{cases} $$

Si $sim(d_j, q) = 1$ entonces el modelo Booleano predice que el documento $d_j$ es relevante para la consulta $q$ (puede que no lo sea). De otra forma, la predicción es que el documento es irrelevante.

El modelo Booleano puede predecir que cada documento es relevante o irrelevante. No existe la noción de coincidencia parcial con la consulta. Por ejemplo, sea un documento $d_{j}$ tal que $\overrightarrow{d_{j}}=(0, 1, 0)$, entonces el documento incluye el término buscado $k_b$, pero se considera irrelevante para la consulta $[q = k_a \wedge (k_b \vee \neg k_c)]$.

Las principales ventajas de este modelo son el formalismo que lo sustenta y su simplicidad. La principal desventaja es que la coincidencia exacta de los términos puede acarrear que se recuperen muy pocos documentos o demasiados, dada la inexperiencia de los usuarios con este tipo de lógica. Puede verse que el modelo de indexado elegido tiene una gran influencia en el posterior proceso de recuperación, lo cual nos lleva al siguiente modelo.

Modelo Vectorial

El modelo vectorial [SL68,Sal71] tiene en cuenta que los pesos binarios son muy limitantes y propone una arquitectura en la cual es posible la coincidencia parcial. Su implementación se lleva a cabo asignando pesos no binarios a los términos de las consultas y de los documentos. Por último, estos pesos se utilizan para calcular el grado de similitud entre cada documento almacenado en el sistema y la consulta del usuario. El modelo tiene en cuenta aquellos documentos que coinciden parcialmente con la consulta, lo que permite que los documentos recuperados se puedan organizar en orden decreciente a su grado de similitud. La principal consecuencia de esto es que el conjunto ordenado de documentos que responden a la consulta es mucho más preciso (en el sentido que hay una mayor coincidencia con las necesidades del usuario) que el conjunto recuperado por el modelo Booleano.

en donde $|{\overrightarrow{d_j}}|$ y $|{\overrightarrow{q}}|$ son las normas del vector que representa al documento $d_j$ y del vector que representa a la consulta $q$ respectivamente. El factor escalar $|{\overrightarrow{q}}|$ no afecta el orden de los documentos porque es constante en todos los documentos, mientras que $|{\overrightarrow{d_j}}|$ es un factor de normalización sobre el espacio de documentos.

Figura 2-3: Una consulta y un documento representados en un espacio vectorial.

Dado que $w(k_i,d_j)\geq 0$ y $w(k_i,q)\geq 0$, entonces $\mathit{sim}(d_{j}, q)\in [0, +1]$, por lo que el modelo no trata de predecir si un documento es relevante o no, sino que los ordena de acuerdo a su grado de similitud con la consulta. Puede recuperarse un documento incluso si sólo coincide parcialmente con la consulta. Por ejemplo, se puede establecer un umbral sobre $\mathit{sim}(d_{j}, q)$ y recuperar todos los documentos con un grado de similitud por encima de ese límite. Para calcular el ranking es necesario especificar cómo obtener los pesos de los términos.

Los pesos de los términos pueden calcularse de distintas maneras. Aquí nos enfocaremos en las más eficientes y/o las utilizados a lo largo de esta tesis, para un análisis más detallado de las distintas técnicas de ponderación de términos puede consultarse [SM83].

La idea está relacionada con los principios básicos de las técnicas de clasificación. Dada una colección de objetos $C$ y una descripción imprecisa de un conjunto $R$, el objetivo de un algoritmo simple de clasificación podría ser separar esa colección en dos subconjuntos: el primero compuesto de objetos que están relacionados con $R$ y el segundo con aquellos que no lo están. En este contexto, una descripción imprecisa significa que no tenemos toda la información necesaria para decidir de forma exacta qué objetos están en $R$ y cuáles no. Un ejemplo de esto es un conjunto de autos $R$ que tienen un precio comparable al de determinada marca y modelo. Dado que no está claro qué significa exactamente el término comparable, no hay una descripción precisa (y única) del conjunto $R$. Otros algoritmos de clasificación más sofisticados podrían intentar separar a los objetos de la colección en varias clases de acuerdo a sus propiedades. Por ejemplo, los pacientes de un doctor especialista en cáncer pueden clasificarse en cinco clases: terminal, avanzado, metástasis, diagnosticado y saludable. Sin embargo, el problema no termina ahí porque es posible que las descripciones de estas clases sean imprecisas y no pueda decidirse en cuál clase debe asignarse a un paciente nuevo. Dado que en general, sólo debe decidirse si un documento es relevante o no, nos referiremos sólo a la primer clase de algoritmos (aquellos que sólo consideran dos clases).

Para ver al problema como uno de clasificación hacemos una analogía con los conjuntos explicados más arriba. Pensaremos a una colección de documentos como una colección de objetos $C$ y a la consulta del usuario como una especificación imprecisa de un conjunto de objetos $R$. Luego debe determinarse cuáles documentos están en $R$ y cuáles no. En un problema de clasificación deben resolverse dos cuestiones principales: primero deben determinarse las características que describen mejor a los objetos de $R$, y segundo, deben determinarse las características que distinguen mejor a los objetos de $R$ de los restantes objetos en $C$. Los algoritmos de clasificación más exitosos son aquellos que balancean los efectos de ambas propiedades. A continuación veremos el método de ponderación de características (o términos) más conocido en el área de IR.

TF-IDF

La forma más natural de describir un documento es a través de los términos que lo componen, mientras más palabras utilicemos, más oportunidades tendremos de recuperar un documento. Esto sugiere que un factor que indique la frecuencia de un término debe estar presente en una métrica de documentos o de consultas [Sal71]. Esta frecuencia se refiere usualmente como el factor TF y proporciona una medida de qué tan bien describe un término al contenido de un documento. Por otro lado, también debe incluirse alguna medida que tenga en cuenta el poder discriminatorio de un término, ya que por ejemplo, el término bebida puede aparecer junto con términos como té, café o cacao en documentos sobre té, café o chocolatada. Puede notarse que el primer término tiene un poder de distinción mucho menor que el de los últimos, por lo que aparecerá en muchos más documentos en una colección. Entonces debe considerarse un factor que ya no dependa de un documento en particular, sino de toda la colección [SJ72]. A este factor se lo refiere usualmente como frecuencia inversa de documentos o factor IDF. La motivación detrás del uso de un factor IDF está dada porque aquellos términos que aparecen en muchos documentos, en general, no son muy útiles a la hora de distinguir a los documentos relevantes de aquellos que no lo son.

Definición 4 [SJ72, BYRN99] Sea $N$ el número de documentos en la colección y $n_i$ el número de documentos en los que aparece el término $k_i$. Sea $\mathit{frec}(k_i,d_j)$ la frecuencia del término $k_i$ en el documento $d_j$, esto es la cantidad de ocurrencias. Entonces, la frecuencia normalizada del término $k_i$ en un documento $d_j$ viene dada por: $$ \mathit{TF}(k_i,d_j) = \frac{\mathit{frec}(k_i,d_j)}{\sum\nolimits_{\forall h}{\mathit{frec}(k_h,d_j)}}\text{.} $$ Puede verse que si el término no aparece mencionado en el documento $d_j$ entonces $\mathit{TF}(k_i,d_j) = 0$. Por otro lado, la frecuencia inversa de documentos viene dada por: $$ \mathit{IDF}(k_i) = log \frac{N}{n_i}\text{.} $$ Los esquemas más conocidos de ponderación de términos utilizan los pesos dados por la siguiente ecuación: $$ w(k_i,d_j) = \mathit{TF}(k_i, d_j) \times \mathit{IDF}(k_i)\text{,} $$ o por alguna variante de esta fórmula. Tales estrategias se llaman esquemas TF-IDF.

Existen algunas variantes de la expresión anterior [SB88] pero, en general, la misma proporciona un buen esquema de ponderación en muchas colecciones.

Las principales ventajas del modelo vectorial son: (1) su esquema de ponderación de términos (TF-IDF) mejora el rendimiento en la recuperación de documentos; (2) su estrategia de coincidencia parcial permite la recuperación de documentos que aproximan a la información pedida por la consulta; y (3) su fórmula de similitud por coseno ordena los documentos de acuerdo a su similitud con la consulta. La desventaja teórica que existe es la independencia mutua que se asumió más arriba (la Ecuación 2-4 no tiene en cuenta las dependencias entre los términos). Sin embargo, en la práctica, tener en cuenta esta dependencia podría volverse en contra ya que, debido a la localidad de muchas dependencias, su utilización indiscriminada en todos los documentos de la colección podría, de hecho, perjudicar el rendimiento global.

A pesar de su simplicidad, este modelo es una estrategia de ranking muy utilizada en las colecciones de documentos generales. Es un modelo que sigue siendo muy popular dado que es rápido y simple. El rendimiento obtenido en sus conjuntos ordenados de respuestas es difícil de mejorar, a menos que se incorpore dentro de la arquitectura del modelo vectorial, alguna estrategia de expansión de consultas o de realimentación de relevancia (ver Subsección 2.2.2).

Modelo Probabilístico

El modelo probabilístico [RJ76] se basa en una arquitectura probabilística. Dada una consulta de usuario, existe un conjunto de documentos que contiene sólo a los documentos relevantes y a ningún otro. Este conjunto de documentos es el conjunto de respuestas ideal. Si tuviéramos la descripción de este conjunto ideal no tendríamos problemas para recuperar estos documentos. Luego, podemos pensar que el proceso de generación de consultas es el proceso de especificación de las propiedades del conjunto ideal (lo cual es, una vez más, análogo a interpretarlo como un problema de clasificación). Pero el problema es que no sabemos cuáles son estas propiedades exactamente. Todo lo que sabemos es que existen términos cuya semántica podría utilizarse para caracterizar esas propiedades. Inicialmente es necesario realizar un esfuerzo por adivinar cuáles podrían ser las propiedades, ya que no las conocemos al momento de realizar la consulta. Estas suposiciones iniciales nos permiten generar una descripción probabilística preliminar del conjunto ideal, la cual se utiliza para recuperar un primer conjunto de documentos. Luego se inicia una interacción con el usuario con el fin de mejorar la descripción probabilística. Tal proceso sería de la siguiente manera.

El usuario analiza los documentos recuperados y decide cuáles son relevantes y cuáles no lo son (aunque, en realidad, no se los analiza a todos, sino a los que se encuentran más arriba en una lista ordenada). Entonces el sistema utiliza esta información para refinar la descripción del conjunto ideal. Repitiendo este proceso se espera que la descripción evolucione y se acerque más a la descripción real. Veamos ahora la siguiente suposición sobre la que se basa el modelo probabilístico.

Suposición (Principio Probabilístico)

Dada una consulta de usuario $q$ y un documento en la colección $d_j$, el modelo probabilístico trata de estimar la probabilidad de que el usuario encuentre interesante al documento $d_j$ (esto es, relevante). El modelo supone que esta probabilidad de relevancia depende solamente de la consulta y del documento. Además, asume que existe un subconjunto de la colección que el usuario acepta como el conjunto que responde a $q$. Ese conjunto ideal se lo etiqueta como $R$ y debería maximizar la probabilidad de relevancia para el usuario. Se predice que los documentos que contiene $R$ son relevantes a la consulta y que los que no están contenidos son irrelevantes.

Para cada documento $d_j$, el modelo asigna como medida de similitud con una consulta $q$ dada, la relación $P(d_j \text{es-relevante-para} q)/P(d_j \text{no-es-relevante-para} q)$, que mide la correspondencia entre que un documento sea relevante y que sea irrelevante para una consulta. Tomando esta relación como un orden, se minimiza la probabilidad de un juicio erróneo [vR79,Fuh92].

Definición 5 [RJ76,BYRN99] En el modelo probabilístico, los pesos de los términos son valores binarios, esto es, $w(k_i,d_j)\in\{0,1\}$ y $w(k_i,q)\in\{0,1\}$. Una consulta $q$ es un subconjunto de términos. Sea $R$ el conjunto conocido de documentos relevantes (o que se suponen relevantes). Sea $\bar{R}$ el complemento de $R$, esto es, el conjunto de documentos irrelevantes. Sea $P(R|\overrightarrow{d_j})$ la probabilidad de que un documento $d_j$ sea relevante a una consulta $q$ y sea $P(\bar{R}|\overrightarrow{d_j})$ la probabilidad de que ese mismo documento no sea relevante para la misma consulta. Entonces la similitud de un documento $d_j$ con la consulta $q$ se define como la relación:$$ \mathit{sim}_{prob}(d_j, q) = \frac{P(R|\overrightarrow{d_j})}{P(\bar{R}|\overrightarrow{d_j})}\text{.} $$

Aplicando la regla de Bayes, $$ \begin{align} \mathit{sim}_{prob}(d_j, q) &= \frac{P(\overrightarrow{d_j}|R)\times P(R)}{P(\overrightarrow{d_j}|\bar{R})\times P(\bar{R})}\text{.} \end{align} $$ En donde,

• $P(\overrightarrow{d_j}| R)$ representa la probabilidad de elegir aleatoriamente a $d_j$ del conjunto de documentos relevantes $R$.
• $P(R)$ representa la probabilidad de elegir aleatoriamente un documento de la colección y que éste sea relevante.
• Las probabilidades sobre $\bar{R}$ son análogas y complementarias.

• $P({k_i}|R)$ representa la probabilidad de que un término $k_i$ esté presente en un documento que se selecciona aleatoriamente de $R$,
• $P(\bar{k_i}|R)$ representa la probabilidad de que un término $k_i$ no esté presente en un documento que se selecciona aleatoriamente de $R$,
• Las probabilidades asociadas a $\bar{R}$ tienen significados análogos a estos.

Recordando que en un principio no se conoce al conjunto $R$, es necesario encontrar un método para realizar los cálculos iniciales de las probabilidades $P(k_i|{R})$ y $P(k_i|\bar{R})$, existiendo varias alternativas para el cómputo.

Al comenzar el proceso, o sea, inmediatamente después de haber especificado la consulta, aún no se han recuperado documentos. Entonces se tienen que hacer algunas suposiciones para simplificar los cálculos: (a) asumir que $P(k_i|{R})$ es constante para todos los términos (p. ej., igual a $0.5$) y (b) asumir que la distribución de los términos a través de los documentos irrelevantes puede aproximarse por la distribución de términos en toda la colección de documentos. Numéricamente esto es: $$ \begin{align*} P(k_i|{R}) &= 0.5 & P(k_i|\bar{R}) &= \frac{n_i}{N}\text{,} \end{align*} $$ donde $n_i$ representa la cantidad de documentos que contienen el término $k_i$ y $N$ el total de documentos en el corpus, respectivamente. Dadas estas suposiciones iniciales, se pueden recuperar documentos que contienen los términos de la consulta y brindan un ranking probabilístico inicial. Luego, se mejora el ranking de la siguiente manera.
Se define un subconjunto, $V$, de los documentos recuperados inicialmente, por ejemplo con los $r$ mejores documentos del ranking, siendo $r$ un umbral definido previamente. Además, sean $V_i \subset V$ aquellos documentos que contienen el término $k_i$. Para mejorar el ranking probabilístico se necesita mejorar $P(k_i|{R})$ y $P(k_i|\bar{R})$, y esto puede realizarse con las siguientes suposiciones: (a) se puede aproximar $P(k_i|{R})$ con la distribución de $k_i$ en los documentos que ya se recuperaron, y (b) se puede aproximar $P(k_i|\bar{R})$ considerando que todos los documentos que todavía no se han recuperado son irrelevantes. Numéricamente, esto es: $$ \begin{align*} P(k_i|{R}) &= \frac{|{V_i}|}{|{V}|} & P(k_i|\bar{R}) &= \frac{n_i - |{V_i}|}{N-|{V}|}\text{.} \end{align*} $$ Repitiendo este proceso recursivamente se van mejorando las probabilidades sin ninguna asistencia del usuario (contrario a la idea original). Sin embargo, puede utilizarse la ayuda del usuario en la selección de los documentos del subconjunto $V$.
Las últimas fórmulas de probabilidad tienen algunos problemas prácticos, como por ejemplo, cuando $V=1$ o $V_i=0$. Para resolverlos se pueden agregar algunos factores de ajuste: $$ \begin{align*} P(k_i|{R}) &= \frac{|{V_i}|+0.5}{|V|+1} & P(k_i|\bar{R}) &= \frac{n_i - |V_i|+0.5}{N-|V|+1}\text{.} \end{align*} $$ Una alternativa al uso de una constante igual a $0.5$, que no siempre es satisfactoria, es utilizar ${n_i}/N$ como factor de ajuste.
$$ \begin{align*} P(k_i|{R}) &= \frac{|V_i|+\frac{n_i}{N}}{|V|+1} & P(k_i|\bar{R}) &= \frac{n_i - |V_i|+\frac{n_i}{N}}{N-|V|+1}\text{.} \end{align*} $$

La principal ventaja del modelo probabilístico es que los documentos son ordenados en orden decreciente de acuerdo a su probabilidad de ser relevante. Las desventajas incluyen: (1) es necesario realizar una separación de los documentos recuperados inicialmente en relevantes e irrelevantes; (2) el método no tiene en cuenta la frecuencia de los términos en los documentos, o sea, los pesos son binarios; y (3) supone la independencia de los términos. Sin embargo, como se dijo en el modelo vectorial, en la práctica no está claro si ésta es una mala suposición.

Modelo de Indexado de Semántica Latente

Al resumir el contenido de los documentos y las consultas por medio de términos se puede producir un bajo rendimiento del proceso de recuperación por dos motivos. El primero es la aparición de documentos irrelevantes en el conjunto de resultados, mientras que el segundo es que los documentos relevantes, que no fueron indexados con ninguno de los términos de la consulta, nunca son recuperados. La razón principal para la aparición de estos efectos es la imprecisión inherente al proceso de recuperación que, como se dijo, está basado en conjuntos de términos clave.

Las ideas en un texto están relacionadas más a los conceptos que describen que a los términos que se utilizan para su descripción. Luego, el proceso de buscar las coincidencias de los documentos con una consulta dada podría basarse en coincidencia de conceptos en lugar de coincidencia de términos. Esto permitiría la recuperación de documentos aun si no estuvieran indexados con los términos de la consulta. El Indexado de Semántica Latente (LSI) es un método que hace uso de estas ideas.

La idea principal en el Modelo de Indexado de Semántica Latente [FDD⁺88,DDL⁺90] es mapear cada vector que representa a un documento y cada vector que representa a una consulta, a un espacio de menos dimensiones que está asociado a conceptos, con la suposición de que el proceso de recuperación en ese espacio reducido puede ser superior a la obtenida en el espacio de términos. Veamos a continuación algunas definiciones.

Definición 6 [FDD+88] Sea $t$ el número de términos índice en la colección y $N$ el número total de documentos. Se define $\overrightarrow{M}=(M_{ij})$ como una matriz de asociación entre términos-documentos con $t$ filas y $N$ columnas. En cada elemento $M_{ij}$ de esta matriz se asigna un peso $w_{i,j}$ asociado al par término-documento $[k_{i},d_{j}]$, $w_{i,j}=w(k_i,d_j)$. Este peso podría calcularse usando TF-IDF.

El proceso de indexado de semántica latente plantea descomponer a la matriz de asociación $\overrightarrow{M}$ en tres componentes, utilizando descomposición en valores singulares, de la siguiente manera: $$ \begin{align*} \overrightarrow{M}=\overrightarrow{K}\overrightarrow{S}\overrightarrow{D^{T}}\text{.} \end{align*} $$ La matriz $\overrightarrow{K}$ es la matriz de autovectores que se deriva de la matriz de correlación término-término, dada por $\overrightarrow{M}\overrightarrow{M^{T}}$, ortonormal por columnas. La matriz $\overrightarrow{D^{T}}$ es la matriz de autovectores que se deriva de la matriz traspuesta de correlación documento-documento, dada por $\overrightarrow{M^{T}}\overrightarrow{M}$, ortonormal por columnas. La matriz $\overrightarrow{S}$ contiene valores singulares en orden decreciente, es diagonal y de tamaño $r\times r$, en donde $r\leq\min(t,N)$ es el rango de $\overrightarrow{M}$. En la Figura 2-5 se muestra de forma esquemática una matriz de $t\times N$ componentes.

Si se descartan los valores singulares más pequeños y sólo se consideran los $s$ valores singulares más grandes de $\overrightarrow{S}$, junto con las columnas correspondientes de $\overrightarrow{K}$ y las filas correspondientes de $\overrightarrow{D^{T}}$, se obtiene una matriz $\overrightarrow{M_s}$ de rango $s$ que es la más cercana a la matriz $M$ original en el sentido de los cuadrados mínimos. Esta matriz está dada por: $$ \begin{align*} \overrightarrow{M_s}=\overrightarrow{K_s}\overrightarrow{S_s}\overrightarrow{D^{T}_s}\text{,} \end{align*} $$ en donde $s$, ${s}<{r}$, es la dimensión del espacio reducido de conceptos. En la Figura 2-6 se muestra el modelo reducido. Al elegir el valor de $s$ se quiere que sea lo suficientemente grande como para preservar toda la estructura presente en los datos originales, pero lo suficientemente pequeño como para descartar los errores de muestreo o los detalles irrelevantes, que están presentes en las representaciones basadas en términos índice. Como puede verse al favorecerse una característica se empeora la otra.

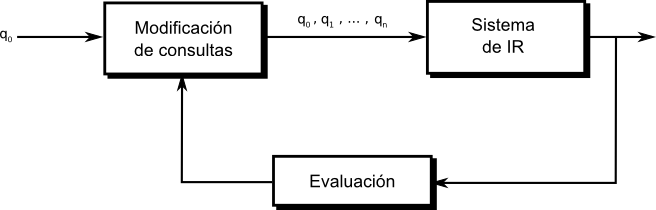
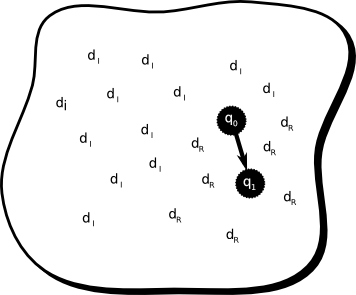
La relación entre dos documentos en el espacio reducido de dimensión $s$ puede calcularse a partir de la matriz $\overrightarrow{M^{T}_s}\overrightarrow{M_s}$ dada por: $$ \begin{align*} \overrightarrow{M^{T}_s}\overrightarrow{M_s} &= (\overrightarrow{K_s}\overrightarrow{S_s}\overrightarrow{D^{T}_s})^{T}\overrightarrow{K_s}\overrightarrow{S_s}\overrightarrow{D^{T}_s}\text{,} && \text{por definición de $\overrightarrow{M}$,}\\ &= \overrightarrow{D_s}\overrightarrow{S_s}\overrightarrow{K^{T}_s}\overrightarrow{K_s}\overrightarrow{S_s}\overrightarrow{D^{T}_s}\text{,} && \text{por propiedad de traspuesta,}\\ &= \overrightarrow{D_s}\overrightarrow{S_s}\overrightarrow{S_s}\overrightarrow{D^{T}_s}\text{,} && \text{por $\overrightarrow{K}$ ortonormal por columnas,}\\ &= (\overrightarrow{D_s}\overrightarrow{S_s})(\overrightarrow{D_s}\overrightarrow{S_s})^{T}\text{,} \end{align*} $$ en donde el elemento $(j,k)$ de la matriz cuantifica la relación entre los documentos $d_j$ y $d_k$.

Para ordenar los documentos respecto de alguna consulta de un usuario se modela la consulta como un pseudodocumento en la matriz de términos-documentos original $\overrightarrow{M}$. Si la consulta es el documento 0 de la matriz original, entonces la primera columna de la matriz $\overrightarrow{M^{T}_s}\overrightarrow{M_s}$ contiene el ranking de todos los documentos respecto de la consulta.

Las matrices que se utilizan en el modelo de indexado de semántica latente son de rango $s$, $s \ll t$ y $s \ll N$, por lo que es un sistema de indexación eficiente de los documentos de una colección, permitiendo además la eliminación de ruido y de redundancia. Además, proporciona un nuevo enfoque al problema de la recuperación de información, basado en la teoría de descomposición en valores singulares.

Una de las limitaciones del LSI es determinar el valor óptimo de $s$. En la mayoría de las aplicaciones $s$ es mucho menor que el número de términos en el índice. Sin embargo, aún no existe una teoría o método para predecir el valor óptimo. Se ha conjeturado que la dimensión óptima es algo intrínseco al dominio de los documentos indexados y, por lo tanto, debe ser determinado empíricamente [LD08]. Los resultados experimentales muestran que la determinación de la dimensión óptima es un problema complejo. En 1991, Susan Dumais, una de las inventoras del LSI, reportó que $s=100$ funcionaba bien para una colección de aproximadamente 1000 documentos, pero también notó que “el número necesario para capturar la estructura de otra colección probablemente dependerá de su tamaño” [Dum91]. Desde ese momento, otros trabajos han especulado que mientras más cantidad de conceptos contenga una colección, más grande deberá ser el valor de $s$ necesario para representarlos adecuadamente. En [Bra08] se analizan los efectos de variar esta dimensión, determinando cómo afecta esto al rendimiento del proceso de recuperación y al costo computacional. Los resultados mostraron que un valor de $s$ entre 300 y 500 es un valor apropiado para obtener un rendimiento estable en colecciones de entre diez mil y varios millones de documentos, por lo que el factor de crecimiento es bastante lento.

A continuación se detallará el proceso de formulación y optimización de consultas. También se explicarán las nociones de relevancia y similitud que serán utilizadas en los capítulos siguientes.

Formulación de consultas

El proceso de formulación de una consulta es complejo y está condicionado a quien lo inicia, a su conocimiento sobre el contenido del repositorio, a su conocimiento acerca de los procesos de indexación y búsqueda, a su familiaridad con el tópico que está buscando, a sus preferencias personales con respecto al vocabulario y a otros aspectos. De hecho, el usuario debe tomar una decisión estadística basándose en su experiencia personal para obtener los resultados que quiere. En cualquier sistema de recuperación la probabilidad a priori de que una consulta satisfaga las necesidades de un usuario varía en gran medida. Por ejemplo, un usuario que conoce de la existencia de un documento dentro de un repositorio, puede formular una consulta que seguramente será exitosa, ya que por ejemplo puede crear una consulta que sea idéntica al documento en cuestión. Como otro caso extremo está el usuario que necesita información sobre un tópico que desconoce por completo. Claramente las probabilidades de que este usuario genere una consulta que recupere el mejor conjunto de documentos son muy bajas.

Por lo tanto en la práctica, las probabilidades de que un sistema satisfaga las necesidades de un usuario son muy variables y, consecuentemente, es importante considerar técnicas que reduzcan esta varianza. Esto puede llevarse a cabo desde dos puntos de vista diferentes. Uno de ellos es desde el punto de vista del usuario, optimizando las consultas para que se minimicen los costos de recuperación, los costos de optimización, y el costo de la información. Por otro lado, también es de interés separar los defectos del proceso de indexación de los defectos producidos por consultas mal formuladas. Es así que los sistemas de IR pueden evaluarse respecto de un conjunto particular de consultas predefinidas, o también es posible definir una consulta óptima para un determinado pedido de información, y de esta forma evaluar mejor el poder de una técnica dada. A continuación se estudiarán algunas técnicas en este sentido.

Reformulación y Optimización de la consulta

Para definir un pedido óptimo es necesario trabajar con una representación explícita del proceso de coincidencia pedido-documento. Una función de coincidencia muy utilizada es la correlación por coseno del pedido con los documentos en el repositorio (Ecuación 2-1). Como se mencionó en la Definición 1, los pesos asignados a los términos de un documento son positivos, por lo que esta correlación induce un orden en los elementos del repositorio que es equivalente a su distancia angular con el vector de la consulta (esto es, $0 \le \mathit{sim}(d_{j}, q) \le 1$ corresponde a una separación angular que va desde 90 a 0 grados sexagesimales).

Dado cualquier pedido (consulta) $q$, asumimos la existencia de un subconjunto $R$ ($R \subset C$) del conjunto de documentos contenidos en el repositorio $C$. Este conjunto es el conjunto de documentos relevantes para el pedido $q$ y debe estar especificado fuera del contexto del sistema de recuperación.

Habiendo definido $R$, un pedido ideal puede ser definido como uno que induce un orden de elementos de $C$ tal que todos los miembros de $R$ están posicionados más altos (o sea que tienen una correlación más alta) que todos los otros elementos de $C$.

El pedido ideal es incierto porque la relevancia es una apreciación subjetiva que, en teoría, la determina el usuario. En tal caso puede decirse que el proceso de indexación no se define desde el punto de vista de un usuario, porque no permite hacer las distinciones que hace un usuario. Por supuesto esto será la norma en lugar de la excepción, ya que la indexación está diseñada para reducir la cantidad de información almacenada en lugar de preservarla. Por esta razón, un pedido óptimo no ambiguo se define como una función de $R$, $C$ y una transformación en el índice la cual es única para cada subconjunto único no vacío $R$ de $C$.

Un pedido óptimo correspondiente a un subconjunto $R$ dado de un repositorio $C$, bajo una transformación del índice $T$, es aquel pedido que maximiza la diferencia entre la media de las correlaciones de los documentos relevantes (miembros de $R$) y la media de las correlaciones de los documentos no relevantes (miembros de $C$ que están en $\bar{R}$).

En términos matemáticos, el vector de un pedido óptimo $\overrightarrow{q_{opt}}$ correspondiente a un conjunto $R \subset C$ está definido como el vector $\overrightarrow{q}$ para el cual:
$$ A = \frac{1}{|R|}\sum\limits_{d_j \in R } {\mathit{sim}(d_{j}, q)} - \frac{1}{|\bar{R}|}\sum\limits_{d_j \in \bar{R} } {\mathit{sim} (d_{j}, q)}\text{,} $$ es máximo, en donde $\mathit{sim}(d_{j}, q)$ es alguna medida de la calidad de los documentos recuperados. Si deseamos tener en cuenta solamente a los pedidos que tienen componentes no negativos en la consulta, entonces el problema se modifica para maximizar $A$ restringido a $w(k_i, q) \ge 0$.
Suponiendo que utilizamos como medida de la calidad de los documentos a la similitud por coseno, substituimos $\mathit{sim}(d_{j}, q)$ de acuerdo a la Ecuación 2-1 y utilizando la notación de vectores, la ecuación anterior queda:
$$ A = \frac{1}{|R|}\left( {\frac{\overrightarrow{q}}{{|\overrightarrow{q}|}}} \right) \cdot \sum\limits_{\overrightarrow{d_j} \in R } {\frac{{\overrightarrow{d_j} }}{{|{ {\overrightarrow{d_j} }| }}}} - \frac{1}{|\bar{R}|}\left( {\frac{\overrightarrow{q}}{{|{ \overrightarrow{q} }|}}} \right) \cdot \sum\limits_{\overrightarrow{d_j} \in \bar{R} } {\frac{{\overrightarrow{d_j} }}{{|{ {\overrightarrow{d_j} } }|}}}\text{,} $$ o
$$\begin{align} A &= \frac{\overrightarrow{q}}{|{\overrightarrow{q}}|}\left[ {\frac{1}{|R|}\sum\limits_{\overrightarrow{d_j}\in R}{\frac{\overrightarrow{d_j}}{{|{\overrightarrow{d_j}}|}}} - \frac{1}{|\bar{R}|}\sum\limits_{\overrightarrow{d_j} \in \bar{R}}{\frac{\overrightarrow{d_j}}{|{\overrightarrow{d_j}}|}}} \right]\text{,}\\ &= \hat{q} \cdot \overrightarrow{v}\text{.}\end{align} $$ En la ecuación de arriba $\hat{q}$ es el vector unitario en la dirección de $\overrightarrow{q}$ y $\overrightarrow{v}$ es un vector igual a la parte encerrada entre corchetes de la ecuación. Claramente, por definición de producto escalar, el $\overrightarrow{q_{opt}}$ es uno en la dirección $\overrightarrow{v}$, o sea $\overrightarrow{q_{opt}} = k\overrightarrow{v}$ (en donde $k$ es un escalar arbitrario), o
$$ \overrightarrow{q_{opt}} = \frac{1}{|R|}\sum\limits_{\overrightarrow{d_j} \in R } {\frac{{\overrightarrow{d_j} }}{{|{ {\overrightarrow{d_j} } }|}}} - \frac{1}{|\bar{R}|}\sum\limits_{\overrightarrow{d_j} \in \bar{R} } {\frac{\overrightarrow{d_j} }{|{ {\overrightarrow{d_j}}}|}}\text{.}$$ Además, es trivial demostrar que $A$ restringido a $w(k_{i},q) \ge 0$ (donde $i$ varía sobre todas las coordenadas de $\overrightarrow{q}$) se maximiza con el vector compuesto por:
$$ w(k_i,q'_{opt}) = \begin{cases} {w(k_i,q_{opt})}\text{,} & \text{para } {w(k_i,q_{opt})} \ge 0\text{,} \\ 0\text{,} & \text{para } {w(k_i,q_{opt})} < 0\text{.}\end{cases} $$ Por lo tanto, con estas suposiciones, existe una consulta óptima no ambigua que se corresponde con cualquier subconjunto no vacío $R$ de $C$. Durante el proceso de evaluación de los sistemas de recuperación automáticos, esta representación de un pedido óptimo: (1) brinda la capacidad de aislar el proceso de indexado de la varianza debido al proceso de formulación de la consulta; (2) mide la habilidad de la transformación del índice para distinguir un conjunto particular de documentos de todos los otros en el repositorio, en donde este conjunto particular se asume que está compuesto por todos los documentos que fueron juzgados como relevantes para algún tópico en particular.

Realimentación de relevancia

La generación de una consulta óptima, que se corresponda con un conjunto particular de documentos, tiene una consecuencia directa en la operación de recuperación de información, dado que el conjunto de documentos en cuestión es el objeto de la búsqueda. Por lo tanto, no hay una forma directa de crear una consulta óptima, ya que si se tiene esa habilidad se elimina la necesidad de la búsqueda. Este tipo de circularidad sugiere una gran analogía con la realimentación en la teoría de control y fue estudiada por Rocchio en los '70s [Roc71b]. Puede verse más claramente la analogía con un sistema de realimentación secuencial si consideramos una secuencia de operaciones de recuperación comenzando con una $q_0$, la cual es luego modificada basándose en la salida que produce el sistema de recuperación (utilizando $q_0$ como entrada), de forma que la consulta modificada $q_1$ esté más cerca de la consulta óptima para ese usuario. Si dejamos que el usuario especifique cuáles de los documentos recuperados son relevantes (los recuperados con $q_0$) y cuáles no, tendremos la señal de error del sistema de IR. Esto puede apreciarse gráficamente en la Figura 2-7. Basándonos en las señales de error y la original es posible producir una consulta modificada de forma tal que la salida esté más cerca de lo que el usuario desea o, de forma que la consulta esté en efecto más cerca de la consulta óptima para ese usuario.

Figura 2-7: Realimentación de relevancia.

Un escenario típico para este proceso involucra los siguientes pasos:

Paso 1:.

Se formula la consulta.

Paso 2:.

El sistema devuelve un conjunto inicial de resultados.

Paso 3:.

Se calcula la relevancia de los resultados obtenidos.

Paso 4:.

El sistema determina una mejor representación de las necesidades de información basándose en esta realimentación.

Paso 5:.

El sistema devuelve un conjunto revisado de resultados.

Dependiendo del nivel de automatización del Paso 3 podemos distinguir tres formas de realimentación que explicaremos más adelante. La efectividad de este proceso dependerá de: (a) qué tan buena es la consulta inicial, ya que los resultados obtenidos deben contener un número razonable de documentos relevantes al tópico que se está buscado; (b) qué tanto vocabulario comparten los documentos relevantes encontrados con los documentos que se están buscando; y (c) qué tan rápido el proceso iterativo converge hacia el óptimo [Har92].

Realimentación Supervisada

La realimentación de relevancia supervisada necesita una realimentación explícita, la cual se obtiene típicamente de usuarios que indican la importancia de cada documento [Roc71b,XA08]. Dada la consulta original $q_0$ y dados los resultados que ella obtuvo como una lista ordenada de acuerdo a su relación con la consulta, el usuario examina esta lista y especifica cuáles son relevantes y cuáles no. Se asume que faltarán algunos resultados relevantes en la lista, por lo que sólo se modificará la consulta con la información que proporciona el usuario. La consulta modificada está compuesta por la $q_0$ más un vector de optimización basado en la información de realimentación. La suposición fundamental de estos sistemas es que el vector resultante será una mejor aproximación que $q_0$ a la consulta óptima y producirá mejores resultados cuando se lo envíe al sistema.

Luego buscamos una relación de la forma:
$$ q_1 = f(q_0, R, \bar{R}), $$ en donde $q_0$ es la consulta original, $R$ es el subconjunto de documentos que el usuario estima que son relevantes y $\bar{R}$ es el subconjunto que estima que no son relevantes. La forma que sugiere esto es:
$$ \overrightarrow{q_1} = \overrightarrow{q_0} + \frac{1}{|R|}\sum\limits_{\overrightarrow{d_j} \in R}{\overrightarrow{d_{j}}} - \frac{1}{|\bar{R}|}\sum\limits_{\overrightarrow{d_j} \in \bar{R}}{\overrightarrow{d_{j}}}\text{,} $$ en donde todos los vectores son unitarios. Luego $\overrightarrow{q_1}$ es el vector que resulta de la suma del vector original más el vector diferencial entre los miembros del conjunto $R$ y los del conjunto $\bar{R}$.
La ecuación anterior puede ser rescrita en la forma:
$$ \overrightarrow{q_1} = {|R|}{|\bar{R}|} \overrightarrow{q_0} + {|\bar{R}|} \sum\limits_{\overrightarrow{d_j} \in R}{\overrightarrow{d_{j}}} - |R| \sum\limits_{\overrightarrow{d_j}\in \bar{R}}{\overrightarrow{d_{j}}}\text{.} $$ Los componentes de $\overrightarrow{q_1}$ pueden restringirse a valores positivos haciendo:
$$ {w(k_i,q'_1)} = \begin{cases} {w(k_i,q_1)}\text{,} & \text{para }{w(k_i,q_1)}\ge 0\text{,} \\ 0\text{,} & \text{para }{w(k_i,q_1)} < 0\text{.} \end{cases} $$ Esto representa la relación básica para la modificación de una consulta utilizando realimentación de relevancia [Roc71b]. Esta relación puede modificarse de distintas maneras imponiendo restricciones adicionales. Por ejemplo, el peso de la consulta original ($|R||\bar{R}|$) puede ser una función de la cantidad de realimentación, de forma tal que con una realimentación alta la consulta original tenga un efecto menor en la consulta final, y, por el contrario, un efecto alto si la realimentación es baja.

El proceso descripto puede hacerse iterativamente y luego, de forma general, puede escribirse:
$$ q_{i+1} =f(q_i, R_i, \bar{R}_i)\text{,}$$ en donde $q_i$ es la $i$-ésima consulta de la secuencia y $R_i$ y $\bar{R}_i$ son los subconjuntos identificados como relevantes e irrelevantes respectivamente, obtenidos como resultado de enviar $q_i$ al sistema de IR.

La consulta original del usuario se utiliza para identificar una región en el espacio del índice, la cual debería contener documentos relevantes. Pero, dado que no existe un conocimiento detallado acerca de las características de los documentos en el repositorio, es poco probable que esa región sea óptima. Luego de que el usuario identifica los documentos relevantes en la región, el sistema tiene suficiente información para intentar generar una consulta mejorada que se centra en los documentos relevantes y, a su vez, maximiza la distancia a los documentos no relevantes. Esto sólo es posible si los conjuntos de documentos relevantes e irrelevantes son diferenciables. Una interpretación gráfica puede verse en la Figura 2-8.

Figura 2-8: Modificación de una consulta basada en la realimentación del usuario.

Una desventaja que se ha encontrado en este método es que requiere que los resultados obtenidos por la primer consulta sean lo suficientemente buenos como para poder encontrar documentos relevantes que guíen al algoritmo hacia la región correcta del espacio de documentos. Esto puede ser un gran problema si el usuario no tiene el suficiente conocimiento del tema que está buscando. También, para que la Ecuación 2-8 funcione correctamente, es necesario que la distribución de términos en los documentos relevantes sea similar y, además, distinta de la existente en los irrelevantes.

Una variante del método de Rocchio es la presentada en [JW04], en donde se compara la consulta con el contexto del usuario. Los autores argumentan que la versión original del algoritmo de Rocchio trabaja solamente basándose en un modelo de usuario que se construye cada vez que se realiza una consulta, y toda información que pudo haberse obtenido en consultas previas se pierde. Es por esto que se utiliza esta información para construir perfiles múltiples del usuario que se preservan a lo largo del tiempo.

Realimentación sin supervisión

Esta variante aplica realimentación de relevancia de forma ciega, sin la asistencia de un usuario que indique cuáles documentos son relevantes y cuáles no. Existen dos tipos básicos de realimentación ciega [HP06]. La primera clase típicamente asume que los $k$ mejores resultados del proceso de búsqueda son relevantes [EL93,BSMS95]. El segundo tipo se ha investigado como una forma alternativa a la realimentación ciega. La expansión de consultas se realiza agregando términos de los $k$ documentos más relevantes recuperados con la consulta original pero, en esta variante, de una colección diferente [KC98,HP06]. Esta colección se suele llamar “colección de expansión”, la cual debe ser razonablemente similar a la colección de “búsqueda”, de otra manera sólo se introduciría ruido. Esta segunda fuente de información incrementa el tamaño total de la colección y aumenta también la probabilidad de tener documentos relevantes en posiciones altas del ranking. Sin embargo, las mejoras obtenidas no han mostrado ser estadísticamente superiores a la primera versión.

Otra forma de expansión de consultas se basa en la utilización de diccionarios de sinónimos^*. Esta técnica expande la consulta utilizando palabras o frases que tienen un significado similar a las que se encuentran en la consulta. Esto aumenta las probabilidades de tener coincidencias con el vocabulario utilizado en los documentos relevantes que se están buscando. Sin embargo, no existen resultados concluyentes acerca de las mejoras en el rendimiento introducidas por el método, incluso si las palabras son elegidas por los usuarios [Voo94].

La creación del diccionario también puede realizarse a partir de los documentos recuperados por la consulta original. En [AF77] los $k$ mejores documentos recuperados se utilizan como una fuente de información sobre la que se construye el diccionario de forma automática. Los términos en esos documentos se agrupan con un algoritmo de clustering y se los trata como cuasi sinónimos. En [CH79] se utiliza esta misma fuente información pero para re-estimar la importancia de los términos en el conjunto de documentos relevantes. Luego, basándose en esta información y sin agregar términos nuevos, se modifican los pesos de los términos de la consulta original. Los experimentos realizados han mostrado mejoras en el rendimiento, pero sólo sobre una colección pequeña. Una alternativa es analizar la colección de documentos de forma completa para generar un diccionario más efectivo [SJ71].

Una generalización exitosa del método de Rocchio es el mecanismo de la Divergencia de la Aleatoriedad (DFR) con estadísticas de Bose-Einstein (Bo1-DFR) [AvR02]. Para aplicar este modelo necesitamos primero asignar un peso a los términos basándonos en su grado de información. Este se estima con la divergencia entre su distribución en los documentos mejor clasificados y en una distribución aleatoria, de la siguiente manera:
$$w(k_i)=\mathit{frec}(k_i) . log_2\frac{1+ P_n}{P_n}+log_2(1+P_n)\text{,}$$ en donde $\mathit{frec}(k_i)$ es la frecuencia del término $k_i$ en los documentos mejor clasificados y $P_n$ es el porcentaje de documentos en la colección que contienen $k_i$. Finalmente, la consulta se expande mezclando los términos más informativos con los términos originales de la consulta.

Realimentación Semisupervisada

En esta última forma de realimentación tampoco es necesaria la intervención del usuario, ya que la relevancia es inferida por el sistema. Una forma de hacer esto es monitorear el comportamiento del usuario. En [SBA07] se propone el uso de una métrica de calidad de búsqueda que mide la “satisfacción” que un usuario obtiene con determinados documentos. La puntuación que el usuario le asigna a los resultados de un motor de búsqueda se tiene en cuenta para mejorar los resultados futuros. Esta realimentación se obtiene de forma implícita, monitoreando las acciones que el usuario realiza normalmente sobre los resultados de una búsqueda, infiriéndose de ellas la realimentación. Esto es una ventaja respecto de la realimentación supervisada que, como se mostrará en la Sección 4.3, es una práctica muy demandante. En particular, en [SBA07] se identifican siete acciones, o características, que es posible monitorear: (a) el orden en que se visitan los documentos; (b) el tiempo que se examina un documento; (c) si se imprime; (d) se guarda; (e) se agrega a Favoritos; o (f) se envía por correo electrónico un documento; y (g) el número de palabras que se copian y pegan en otra aplicación. Estas características se utilizan para obtener el nivel de importancia que el usuario le asigna a un documento para una consulta dada. Este proceso continúa en el tiempo y va mejorando el conocimiento que tiene el sistema sobre las necesidades del usuario y, por lo tanto, le ayudará a obtener resultados cada vez más acordes a él.

Algunas de estas características ya habían sido utilizadas en otros trabajos previos, una clasificación puede encontrarse en [KT03]. En [Joa02] se utiliza la información histórica de los clicks de los usuarios, sobre los resultados de un motor de búsqueda, para entrenar un clasificador y así mejorar el ranking de varios motores web. En [WJvRR04] se hizo también una simulación para determinar la efectividad de distintos modelos de realimentación basados en los clicks de los usuarios. Los modelos analizados fueron votación binaria, varios modelos probabilísticos y un modelo aleatorio. Los documentos de los resultados se presentaron con distintas granularidades, desde solamente el título y algunas sentencias hasta el texto completo, y dependiendo de la granularidad elegida por el usuario, el sistema aprendía qué objetos eran más relevantes para una consulta. En [SHY04] se utilizan perfiles de usuario colaborativos basados en la historia de navegación de los usuarios para mejorar los resultados de una búsqueda.

En [KB04] se utilizó el tiempo que emplea un usuario para explorar un documento como una forma de realimentación, mostrando que esta es una característica muy subjetiva y que deben aprenderse las preferencias de cada usuario en particular para lograr los mejores resultados. En [ACR04] se introduce la noción de robustez, ya que, aunque en muchos casos la expansión de consultas tiene éxito, en otros empeora la calidad de los documentos recuperados. Si se mide solamente el rendimiento global de un sistema, se obtiene una imagen del comportamiento promedio, pero no es posible analizar la varianza de los resultados y se pueden estar obviando resultados muy pobres en algunas consultas. Los autores notaron que las consultas que presentaban un peor rendimiento, aun sin la utilización de expansión de consultas, empeoraban al habilitar esta característica. Por lo tanto introducen, en la conferencia TREC (Subsección 3.1.5), una métrica que predice cuándo la expansión resultará beneficiosa y cuándo no, logrando mejoras significativas sobre el método estándar.

Capítulo 2-2 ->